Question

A bar of cross-section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle $\theta $ with a plane at right angles to the bar. Then shearing stress will be maximum if $\theta $

Answer 1

Hint:Consider the tensile force to be a normal force. For shearing stress, we consider forces which are parallel to the plane of the bar. Consider the equilibrium on the plane of the given bar. Split the force F along the plane and perpendicular to the plane. Shearing stress is the ratio of the parallel component of the force divided by the area.

Complete step by step solution:
Consider the following diagram:

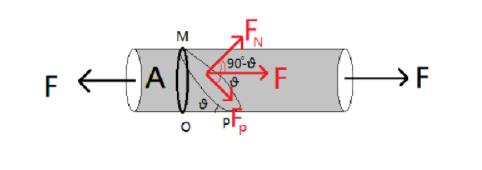
As two forces are acting on the rod, shear will act on the rod and eventually there will be some change in dimension of the rod. Let the plane MP be at equilibrium. Now force F is acting on this plane. Let this force make an angle $\theta $ with the equilibrium plane.

Now, the component of force along the equilibrium plane will be:

${F_p} = Fcos\theta $ --equation $1$

Here, $F$ is the force acting on the equilibrium plane.
$\theta $ is the angle that this force makes along with the equilibrium plane.

We need to find at which angle the shearing stress is maximum. Shearing stress is given as the ratio of the component of force parallel to the equilibrium plane. The area under consideration is the area of the plane along MP.

We have the area of the cross section of the rod, $A$ .

The component of the area along the plane will be: $Acosec\theta $ from
$\vartriangle MOP$

Shearing stress $ = \dfrac{{Fcos\theta }}{{Acosec\theta }}$

$ \Rightarrow Shearing\,stress = \dfrac{{Fsin\theta cos\theta }}{A}$
$ \Rightarrow Shearing\,stress = \dfrac{{2sin\theta cos\theta }}{{2A}} \times F$
multiply and divide by $2$

$ \Rightarrow Shearing\,stress = \dfrac{{F\sin 2\theta }}{{2A}}$

Shearing stress will be maximum when $\sin 2\theta $ is maximum.
$ \Rightarrow \sin 2\theta = 1$
$ \Rightarrow \theta = 4{5^ \circ }$

Therefore, for $\theta = 4{5^ \circ }$ the shearing stress will be maximum.

Note:Shearing stress is the force that tends to change the dimension of the given object. In this case, we have considered the area of cross section to be deformed at an angle $\theta $ . Shearing stress is the ratio of tangential force to the area along the plane.