Question

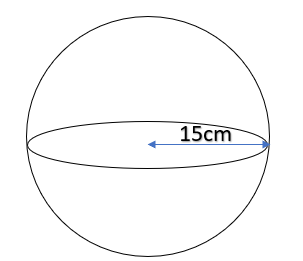
A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimeters of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15cm.

Answer 1

Hint-In this question, the rate of pumping is given to us. Directly use formula for volume of sphere and find the rate of change of volume of sphere with respect to time(t) solve for rate of change of radius with respect to time(t).

Complete step by step answer:
Volume of sphere, V = $\dfrac{4}{3}\pi {r^3}$
Rate of change of volume V w.r.t to time(t)=
$
  \dfrac{{dv}}{{dt}} = \left( {\dfrac{{dv}}{{dr}}} \right) \times \left( {\dfrac{{dr}}{{dt}}} \right) \\
  \dfrac{{dv}}{{dt}} = \dfrac{4}{3}\pi \times 3{r^2} \times \dfrac{{dr}}{{dt}} \\
  \dfrac{{dv}}{{dt}} = 4\pi {r^2}\dfrac{{dr}}{{dt}} \\
$
Given, $
  \dfrac{{dv}}{{dt}} = {\text{ Rate of pumping = 900c}}{{\text{m}}^3}/s \\
  {\text{and }}r = 15cm \\
$
$
   \Rightarrow \dfrac{{dv}}{{dt}} = 4\pi \times \left( {{{15}^2}} \right)\left( {\dfrac{{dr}}{{dt}}} \right) \\
  900 = 900\pi \left( {\dfrac{{dr}}{{dt}}} \right) \\
  \left( {\dfrac{{dr}}{{dt}}} \right) = \dfrac{{900}}{{900\pi }} = \dfrac{1}{\pi }cm/s \\
$
Note- In order to solve such types of problems students must remember the formula for the volume of common geometrical shapes such as sphere. The major source of mistakes in such types of problems is due to the difference in the units given at different places, so students must take extra care of the units mentioned. Students should try to convert all the values in one common unit to avoid mistakes.