Question

A balloon is observed simultaneously from three points $A,B,C$ on the straight road directly under it. The angular elevation at \[B\] is twice that of $A$ and the angular elevation at $C$ is thrice that of $A$. If the distance between $A$ and $B$ is $200m$ and the distance between $B$ and $C$ is $100m$, find the height of the balloon.
A. $50\sqrt 3 m$
B. $50m$
C. $150\sqrt 3 $$m$
D, $100\sqrt 3 m$

Answer 1

Hint:In this question, we will firstly draw the figure according to the given information. We will locate the points $A,B,C$ on the straight line and then try to find out the relations in the angle of elevation with respect to the three given points. We will use the trigonometric functions and then use the distance between the points, we will easily get the height of the balloon.

Complete step-by-step answer:

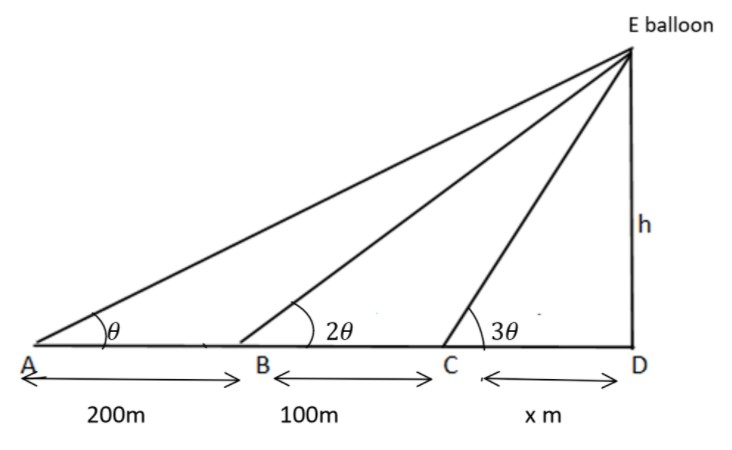
Given $A,B,C$ are the three points on the straight road and a balloon is observed from the three points. The angular elevation at \[B\] is twice that of $A$. Let the angle of elevation at $A$is $\theta $, then the angle of elevation at $B$ is $2\theta $. Also the angular elevation at $C$ is thrice that of $A$, so it will be $3\theta $.
Hence the angle of elevation at $A,B,C$ are $\theta ,2\theta ,3\theta $.
So, the above is the diagram for this question.
From given information we distance between $A$ and $B$ is $200m$, so
$AB = 200m$$ - - - - - (1)$
Similarly, it is given that distance between $B$ and $C$ is $100m$, so
$BC = 100m$$ - - - - - (2)$
Let distance between $C$ and $D$ is $x$, that is,
$CD = x$$ - - - - - (3)$
Let height of the balloon be $ED = h - - - - - (4)$
Now according to the question, we have to find the height of the balloon that is, $h$
Now, it is clear from the above figure that height of the balloon is perpendicular for the right-angled triangles EDC, EDB and EDA. Using trigonometric formulas for these right-angled triangles we will get some equations involving $h$ and by solving these equations we can easily get the value of $h$.
Now let’s work according to above procedure-
And firstly, taking triangle EDC,
We can clearly see from the figure that $EDC$ is a right-angled triangle.
We know $\tan \theta = \dfrac{{{\text{prependicular}}}}{{{\text{base}}}}$, now using it for angle $3\theta $, we get,
So, $\tan 3\theta = \dfrac{{perpendicular}}{{base}} = \dfrac{{ED}}{{CD}}$
Using (3) and (4) and substituting values of $ED{\text{ and }}CD$, we get,
$\tan 3\theta = \dfrac{h}{x}$
Now simplifying it further we get
$x = \dfrac{h}{{\tan 3\theta }}$
Using $\cot 3\theta = \dfrac{1}{{\tan 3\theta }}$, we get
$x = h\cot 3\theta - - - - - - (5)$
 Secondly, consider the right-angled triangle $EDB$ and again using, $\tan \theta = \dfrac{{perpendicular}}{{base}}$ for angle $2\theta $, we get
$\tan 2\theta = \dfrac{{ED}}{{BD}}$
Now using (2) to substitute value of ED and using figure we can say $BD = BD + CD$, we get,
$
  \tan 2\theta = \dfrac{h}{{BC + CD}} \\
  BC + CD = \dfrac{h}{{\tan 2\theta }} \\
 $
Now we know that, $\dfrac{1}{{\tan \theta }} = \cot \theta $, we get,
$BC + CD = h\cot 2\theta $
Using (2) and (3) and substituting $BC = 100m$ and $CD = x$, we get,
\[100 + x = h\cot 2\theta - - - - (6)\]
Now taking the triangle $EDA$ right-angled at D,
Again using, $\tan \theta = \dfrac{{perpendicular}}{{base}}$
$\tan \theta = \dfrac{{ED}}{{AD}}$
Now using figure, we can directly see $AD = AB + BC + CD$ and using (2) to substitute value of ED, we get
$\tan \theta = \dfrac{h}{{AB + BC + CD}}$
Now using (1), (2) and (3) to substitute values of AB, BC and CD, we get
$
  \tan \theta = \dfrac{h}{{200 + 100 + x}} = \dfrac{h}{{300 + x}} \\
   \Rightarrow \tan \theta = \dfrac{h}{{300 + x}} \\
 $
Now further solving it, we get
$300 + x = \dfrac{h}{{\tan \theta }}$
Now again, $\dfrac{1}{{\tan \theta }} = \cot \theta $, we get,
$300 + x = h\cot \theta - - - - - (7)$
Now subtracting equation (5) from (6), we get
$100 + x - x = h\cot 2\theta - h\cot 3\theta $
$100 = h\left( {\cot 2\theta - \cot 3\theta } \right) - - - - - (8)$
Now subtracting equation (6) from (7), we get
$200 = h\left( {\cot \theta - \cot 2\theta } \right) - - - - - (9)$
Now dividing equation (8) by (9),
$\dfrac{{100}}{{200}} = \dfrac{{h\left( {\cot 2\theta - \cot 3\theta } \right)}}{{h\left( {\cot \theta - \cot 2\theta } \right)}}$
Now $h$ is cancelled from numerator and denominator, we get
$\dfrac{1}{2} = \dfrac{{\left( {\cot 2\theta - \cot 3\theta } \right)}}{{\left( {\cot \theta - \cot 2\theta } \right)}}$
Now using, $\cot \theta = \dfrac{{\cos \theta }}{{\sin \theta }}$ for $\cot \theta ,\cot 2\theta {\text{ and }}\cot 3\theta $, we get,
$\dfrac{1}{2} = \dfrac{{\dfrac{{\cos 2\theta }}{{\sin 2\theta }} - \dfrac{{\cos 3\theta }}{{\sin 3\theta }}}}{{\dfrac{{\cos \theta }}{{\sin \theta }} - \dfrac{{\cos 3\theta }}{{\sin 3\theta }}}}$
$\dfrac{{\cos \theta }}{{\sin \theta }} - \dfrac{{\cos 3\theta }}{{\sin 3\theta }} = 2\left\{ {\dfrac{{\cos 2\theta }}{{\sin 2\theta }} - \dfrac{{\cos 3\theta }}{{\sin 3\theta }}} \right\}$
Now taking L.C.M., we get,
$\dfrac{{\sin 2\theta \cos \theta - \sin \theta \cos 2\theta }}{{\sin \theta \sin 2\theta }} = \dfrac{{2(\sin 3\theta \cos 2\theta - \sin 2\theta \cos 3\theta )}}{{\sin 2\theta \sin 3\theta }}$
Now cancelling $\dfrac{1}{{\sin 2\theta }}$ from both sides, we get
$\dfrac{{\sin 2\theta \cos \theta - \sin \theta \cos 2\theta }}{{\sin \theta }} = \dfrac{{2(\sin 3\theta \cos 2\theta - \sin 2\theta \cos 3\theta )}}{{\sin 3\theta }}$
Now using, $\sin A\cos B - \sin B\cos A = \sin (A - B)$, where for L.H.S $A = 2\theta {\text{ and }}B = \theta $ and for R.H.S $A = 3\theta {\text{ and }}B = 2\theta $, we get,
$\dfrac{{\sin (2\theta - \theta )}}{{\sin \theta }} = \dfrac{{2\sin (3\theta - 2\theta )}}{{\sin 3\theta }}$
$\dfrac{{\sin \theta }}{{\sin \theta }} = \dfrac{{2\sin \theta }}{{\sin 3\theta }}$
$1 = \dfrac{{2\sin \theta }}{{\sin 3\theta }}$
Now solving further, we get,
$\dfrac{{\sin 3\theta }}{{\sin \theta }} = 2$
Now using formula,
$\sin 3\theta = 3\sin \theta - 4{\sin ^3}\theta $ and substituting value of $\sin 3\theta $, we get
$\dfrac{{3\sin \theta - 4{{\sin }^3}\theta }}{{\sin \theta }} = 2$
Now taking $\sin \theta $ common from numerator, we get,
$\dfrac{{\sin \theta (3 - 4{{\sin }^2}\theta )}}{{\sin \theta }} = 2$
Now cancelling $\sin 3\theta $ from L.H.S, we get
$3 - 4{\sin ^2}\theta = 2$
$1 - 4{\sin ^2}\theta = 0$
Now further solving we get
${\sin ^2}\theta = \dfrac{1}{4}$
$ \Rightarrow \theta = \dfrac{\pi }{6}$
Substituting $\theta = \dfrac{\pi }{6}$ in equation (9), $200 = h\left( {\cot \theta - \cot 2\theta } \right)$ to get value of $h$
So,
$200 = h(\cot \dfrac{\pi }{6} - \cot \dfrac{\pi }{3})$
Now substituting $\cot \dfrac{\pi }{6} = \sqrt 3 $ and $\cot \dfrac{\pi }{3} = \dfrac{1}{{\sqrt 3 }}$, we get,
$200 = h(\sqrt 3 - \dfrac{1}{{\sqrt 3 }})$
By solving this above equation, we get,
$\dfrac{{200}}{{(\sqrt 3 - \dfrac{1}{{\sqrt 3 }})}} = h$
Now solving it further, we get,
$
   \Rightarrow h = \dfrac{{200}}{{\left( {\dfrac{{3 - 1}}{{\sqrt 3 }}} \right)}} = \dfrac{{200\sqrt 3 }}{2} \\
   \Rightarrow h = 100\sqrt 3 \\
 $
Hence $h = 100\sqrt 3 m$

So, the correct answer is “Option D”.

Note:In the above problem we use the trigonometric function which should involve perpendicular and the base. So we use \[\tan \theta \]. And here we need to find the height and the base from a given right angled triangle. And we should try to understand which trigonometric function we should apply in order to get the desired result.