Question

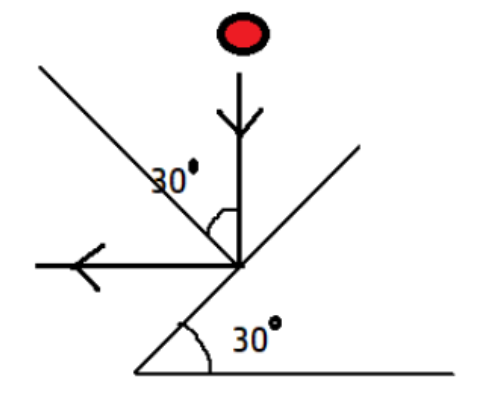
A ball is released from a point, it goes vertically downwards and collides with a fixed smooth inclined plane of angle of inclination of 30 \[{}^\circ \]from the restitution between the ball and the inclined plane is

(A) \[\dfrac{1}{2}\]
(B) \[\dfrac{1}{3}\]
(C) 1
(D) none of these

Answer 1

Hint:A ball collides with an inclined plane of inclination \[30{}^\circ \] after falling through a distance, since it moves horizontally just after the impact. We can use here the concept of coefficient of restitution to arrive at the solution.

Complete step by step answer:
A ball is just dropped say from a height h,
To find the velocity at the impact using the third equation of motion we get,
\[\begin{align}
& {{v}^{2}}-{{u}^{2}}=2gh \\
&\therefore v=\sqrt{2gh} \\
\end{align}\]
Now let us resolve the velocity vector,

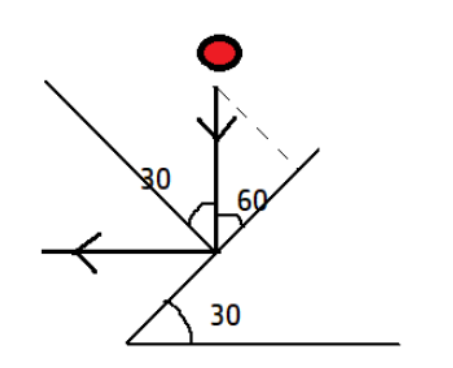
Component of velocity parallel to the plane is \[v\cos 60\]= \[\dfrac{v}{2}\]
Component of velocity perpendicular to the plane is \[v\sin 60=\dfrac{v\sqrt{3}}{2}\]
From the figure, it is clear that velocity parallel to the plane remains the same since the rebound velocity is horizontal,
Coefficient of restitution, e= \[\dfrac{{{v}_{2}}}{{{v}_{1}}}=\dfrac{v\cos 60}{v\cos 30}=\dfrac{1}{3}\]

So the value of e comes out to be \[\dfrac{1}{3}\]. Hence, the correct option is (B).

Additional Information:
The coefficient of restitution denoted by (e) is the ratio of the final to initial relative velocity. It indicates how much kinetic energy remains after a collision between two bodies. It normally ranges from 0 to 1 where 1 would be a perfectly elastic collision. For a perfectly elastic collision, it would mean the final and initial velocities are the same and that means the complete transfer of energy but that is an ideal case.

Note: Here we have resolved the velocities because the ball after being dropped is striking an inclined plane which is inclined at a given angle. We must be careful while resolving the given vector. The initial velocity is taken zero because the ball was dropped.