Question

A ball is dropped from the top of a tower of height \[100{\text{ }}m\] and at the same time another ball is projected vertically upwards from ground with a velocity \[25{\text{ }}m{s^{ - 1}}.\] Then the distance from the top of the tower, at which the two balls meet is.
A. \[68.4{\text{ }}m\]
B. \[48.4{\text{ }}m\]
C. \[18.4{\text{ }}m\]
D. \[28.4{\text{ }}m\]
E. \[78.4{\text{ }}m\]

Answer 1

Hint: - We can clearly get the idea from the question that the total distance travelled by those two balls is equal to the height of the tower.
- To find out the distance travelled by those balls we can use $s = ut + \dfrac{1}{2}a{t^2}$.
- For the first ball, the initial velocity is $0$. It will move with an acceleration of $9.8m{s^{ - 2}}$.

- For the second ball, the initial velocity is $25m{s^{ - 1}}$. It will move with a retardation of $9.8m{s^{ - 2}}$.
- Those two balls will travel for equal time.

- We have to find out the distance travelled by those two balls in time $t$. Sum of those distances travelled by those two balls is equal to the total height of the tower.

-From that we will get the value of $t$.
-Now, putting the value of $t$ in $s = ut + \dfrac{1}{2}a{t^2}$ for the second ball, we can easily get the answer.

Complete step by step answer:
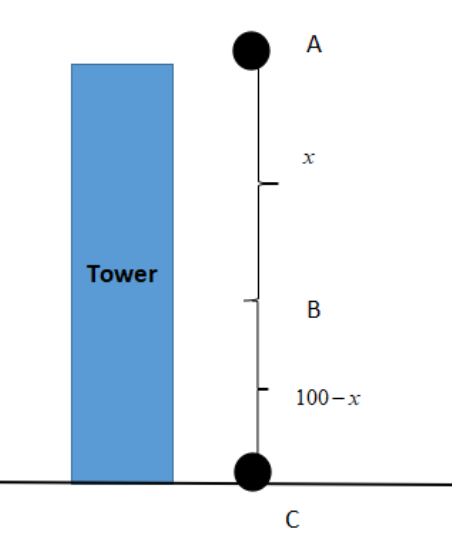
Let (A) denotes the top of the tower and (C) denotes the foot of the tower. And (B) is the point where those balls met each other after time $t$.

Let, the distance travelled by the first ball in time $t$, \[AB{\text{ }} = \] $x$
As, the total height of the tower is $100m$.

So, the second ball has to cover a distance of $100 - x$ in the same time if it has to meet the first ball.
\[BC{\text{ }} = \] $100 - x$

For first ball,

Initial velocity, $u = 0$\[\left( {{\text{ }}As,{\text{ }}it{\text{ }}was{\text{ }}released{\text{ }}from{\text{ }}the{\text{ }}top{\text{ }}of{\text{ }}the{\text{ }}tower} \right).\]
It will fall down with gravitational acceleration, $g = 9.8m{s^{ - 2}}$.
And, we have assumed that it has travelled $x$ distance in time $t$.

So, using the formula $s = ut + \dfrac{1}{2}a{t^2}$

Where $s$ is the distance travelled in time $t$, $u$ is the initial speed and $a$ is the acceleration.
Putting those values,
$x = 0 \times t + \dfrac{1}{2} \times 9.8 \times {t^2}$
$ \Rightarrow $ $x = 4.9{t^2}$ …………………………….(1)

For second ball,

Again to get the distance travelled by the second ball we have to use, $s = ut + \dfrac{1}{2}a{t^2}$.
Where,
Initial velocity, $u = 25m{s^{ - 1}}$.
And the ball is travelling for time $t$ but with a retardation (as gravitational force on the ball is acting opposite to the motion of the ball) of $9.8m{s^{ - 2}}$.
So,$a = - 9.8m{s^{ - 2}}$
An, already we have assumed the distance travelled by the ball is $(100 - x)$.

So, $100 - x = 25 \times t + \dfrac{1}{2} \times ( - 9.8) \times {t^2}$
$ \Rightarrow $ $100 - x = 25t - 4.9{t^2}$
$ \Rightarrow $ $100 - 4.9{t^2} = 25t - 4.9{t^2}$ \[\left[ {Using{\text{ }}equation{\text{ }}\left( 1 \right)} \right]\]
$ \Rightarrow $ $100 = 25t$
$ \Rightarrow $ $25t = 100$
$ \Rightarrow $ $t = \dfrac{{100}}{{25}} = 4$

So, after $t = 4s$ those two balls will meet each other.

Now, putting the value of $t$ in equation (1),
$x = 4.9 \times {4^2} = 4.9 \times 16 = 78.4m$

So, they will meet each other at (B), which is $78.4m$distance away from the top.

So, the correct answer is “Option E”.

Note:
- If velocity of any object is increasing, it means that object is moving with positive acceleration.
- And, if velocity of any object is decreasing, it means that object is moving with negative acceleration or retardation.
- We should take care while putting the value of acceleration in any equation. Students should check whether velocity of that object is decreasing or not.
- Students should take care of units. Before putting all data in the equation we should convert all units in the SI unit system.