Question

A ball collides with a fixed inclined plane of inclination \[\theta \] after falling through a distance \[h\]. If it moves horizontally just after the impact, the coefficient of restitution is:
A. \[\tan \theta \]
B. \[{\tan ^2}\theta \]
C. \[\cot \theta \]
D. \[{\cot ^2}\theta \]

Answer 1

Hint:We are to find the value of coefficient of restitution, for that recall the formula for coefficient of restitution. Using the given conditions, find the values of initial and final velocities of the ball just before the collision and just after the collision respectively. Use these values to find the value of coefficient of restitution.

Complete step by step answer:
Given, the inclination of the plane is \[\theta \]. Height from which the ball fell is \[h\]. We are asked to find the coefficient of restitution. Coefficient of restitution is the ratio between the final velocity and initial velocity.

Let us first draw a neat diagram for the problem.

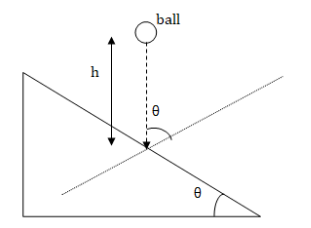
We draw a normal on the plane at the point where the ball hits, we observe it makes angle \[\theta \] with the direction of the ball.
Let \[u\]be the velocity of the ball before colliding with the plane.
From the diagram, we observe velocity of approach is \[u\cos \theta \].

It is given the ball moves horizontally just after impact. So we observe from the diagram, the final velocity will be \[u\sin \theta \].

We have the formula for coefficient of restitution as,
\[e = \dfrac{{{\text{final velocity}}}}{{{\text{initial velocity}}}}\]
Now, putting the values of final and initial velocities we get
\[e = \dfrac{{u\sin \theta }}{{u\cos \theta }} \\
\Rightarrow e = \tan \theta \]
Therefore, the coefficient of restitution is \[\tan \theta \].

Hence, the correct answer is option A.

Note: In the given question, the plane with which the ball collides was at rest before and after collision so coefficient of restitution was just the ratio between the final and initial velocities of the ball. But there may be some cases in which two bodies both moving with some velocities collide with each other and after collision there velocities changes, in that the coefficient of restitution is written as the ratio of final relative velocity of the two bodies and initial relative velocity of the two bodies. That is, \[e = \dfrac{{{v_2} - {v_1}}}{{{u_2} - {u_1}}}\] where \[{u_1}\] and \[{u_2}\] are the initial velocity of the bodies , \[{v_1}\] and \[{v_2}\] are the final velocity of the bodies.