Question

A, B and C are three collinear points on the ground such that B lies between $A$ and \[C\] and \[AB = 10m\]. If the angles of the elevation of the top of a vertical tower standing at \[C\] are respectively ${30^ \circ }$ and ${60^ \circ }$ as seen from \[A\] and \[B\], then find the height of the tower.

Answer 1

Hint: In this problem we are going to make a diagram first and then taking trigonometric relations in different right triangles. We consider the given problem step by step and try to make a diagram for finding the height of the tower. In this, we will use the formula of trigonometric ratios. And the formula is given below.

Formula Used:
${{tan(\theta) = }}\dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}}$

Complete step by step answer:

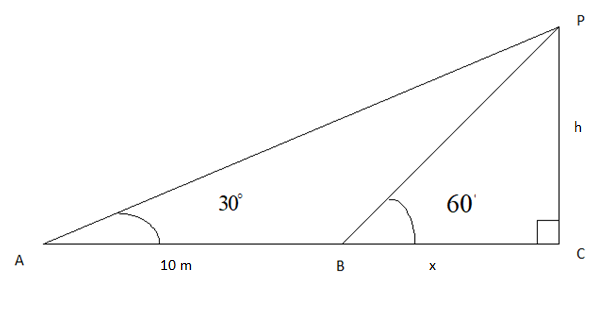
According to the question \[AB\] is equal to \[10m\]; we have to find the height of the tower that is \[PC\] in the diagram. Using trigonometric relation we have to find the length of \[PC\]
Let us assume that \[h\] is the height of the tower which is \[PC\].
And also let \[BC\] as \[x\].
Since in the diagram $\Delta PAC$ and triangle $\Delta PBC$ is right angles triangle so we can apply trigonometric relations in those triangles.
Now, in $\Delta PAC$,
We have given that \[AB = 10m\] and we have assumed \[BC\] as \[x\] so,
\[AC\] will be equal to sum of \[AB\] and \[BC\], that is
\[AC = AB + BC\]
$AC = (10 + x)\,{\text{m}}$
Now, we apply trigonometric relations
$\tan A{\text{ = }}\dfrac{{{\text{Side opposite to angle A}}}}{{{\text{Side adjacent to angle A}}}}$
Here Angle \[A\] is ${30^ \circ }$ and \[AC\] which is calculated above is $(10 + x)$ and height of tower is assumed as \[h\]
Now, putting the values we get,
$\tan {30^ \circ } = \dfrac{h}{{10 + x}}$
Since, we know that$\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$, Values of the trigonometric ratios at specific angles
Putting the value we get,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{10 + x}}$
Now cross multiply the equation we get,
$10 + x = h\sqrt 3 $
Subtracting above equation by 10,
$x = h\sqrt 3 - 10$------------------------ [1]
Now, in \[\Delta PBC\],
We have assume \[BC\] as \[x\] and \[PC\] as \[h\],
Now, we apply trigonometric relations
$\tan {\text{B = }}\dfrac{{{\text{Side opposite to angle B}}}}{{{\text{Side adjacent to angle B}}}}$
Here opposite side is \[PC\] and adjacent side is \[BC\] and angle \[B\] is ${60^ \circ }$ putting these we get,
$\tan {60^ \circ } = \dfrac{h}{x}$
Using the value of $\tan {60^ \circ } = \sqrt 3 $as trigonometric ratios of specified angles in diagram${\text{ED = h + 60}}$,
Putting above values in equation we get,
$\sqrt 3 = \dfrac{h}{x}$
Now cross multiply above equation we get,
$x = \dfrac{h}{{\sqrt 3 }}$----------------------- [2]
Now comparing the values of \[x\] from above two results in equation [1] and equation [2]
We get,
$h\sqrt 3 - 10 = \dfrac{h}{{\sqrt 3 }}$
Now, subtracting above equation by $\dfrac{h}{{\sqrt 3 }}$ and adding both sides by 10 we get,
 $h\sqrt 3 - \dfrac{h}{{\sqrt 3 }} = 10$
Now, taking LCM on left hand side we get,
\[\dfrac{{3h - h}}{{\sqrt 3 }} = 10\]
Subtraction \[h\] from \[3h\] and multiplying equation with \[\sqrt 3 \] we get,
\[2h = 10\sqrt 3 \]
Now dividing both sides by 2 we get, \[h = 5 \times 1.732m\]
\[h = 5\sqrt 3 m\]
Putting the value of \[\sqrt 3 \] as 1.732 we get,
\[h = 5 \times 1.732m\]
We get,
\[h = 8.66{\text{ }}m\]

$\therefore$ The height of the tower is \[8.66m\].

Note:
We have to make a diagram and after that, we have to analyze what is given in the problem and what we have to find out. And use the correct values for the ratios for specified triangles. Note that you should be careful while marking angle.