Question

‘A’ and ‘B’ are two pegs on a vertical wall along a horizontal line separated by a distance of $ 13cm $ . A body of mass $ 169kgwt $ is suspended by a thread of $ 17cm $ connected between ‘A’ and ‘B’ such that the two segments of strings are perpendicular to each other. Find the tensions in shorter and longer parts of the string.

Answer 1

Hint: For solving this sum, it is firstly needed to draw the diagram. Then, apply Pythagoras theorem to calculate the length of two sides of the string. After that identify that the horizontal components of the tension cancel each other and the vertical components balance the weight of the suspended body and deduce an equation for mathematically representing it. By solving these two equations we will get the magnitude of the tension in two strings.

Formula used:
Pythagoras Theorem: $ {\left( {Base} \right)^2} + {(Perpendicular)^2} = {(Hypotenuse)^2} $

Complete step by step answer:
From the given question we have the following information:
Distance between two pegs $ = 13cm $
Total length of the thread by which the body is suspended $ = 17cm $
Mass of the body $ (m) = 169kgwt $
It is also given that the two segments of strings are perpendicular to each other.
Let us represent the suspended body as $ C $ . The tension in the two parts of the string be $ T $ and $ T' $ . Let $ DE $ be a horizontal line drawn. Now let us visualize how the diagram would look like.

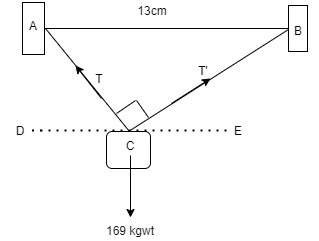
As it is a right-angled triangle, we can apply Pythagoras theorem to find out the magnitude of sides $ AC $ and $ CB $ . As the total length is $ 17cm $ , let us take one side as $ xcm $ and another side as $ (17 - x)cm $ .
So, applying Pythagoras theorem we have,
 $ {\left( {AC} \right)^2} + {\left( {BC} \right)^2} = {\left( {AB} \right)^2} $
 \[ \Rightarrow {x^2} + {(17 - x)^2} = {(13)^2}\]
 $ \Rightarrow {x^2} + 289 - 34x + {x^2} = 169 $
 $ \Rightarrow 2{x^2} - 34x + 289 - 169 = 0 $
 $ \Rightarrow 2{x^2} - 34x + 120 = 0 $
 $ \Rightarrow {x^2} - 17x + 60 = 0 $
 $ \Rightarrow (x - 12)(x - 5) = 0 $
 $ \Rightarrow {x_1} = 5cm;{x_2} = 12cm $
If we consider $ \angle ACD = {\theta _1} $ and $ \angle BCE = {\theta _2} $ then from geometry we can say that $ \angle CAB = {\theta _1} $ and $ \angle ABC = {\theta _2} $ respectively as they are alternate interior angles.
Thus, we can write:
 $ \cos {\theta _1} = \dfrac{5}{{13}} $ ; $ \cos {\theta _2} = \dfrac{{12}}{{13}} $ ; $ \sin {\theta _1} = \dfrac{{12}}{{13}} $ ; $ \sin {\theta _2} = \dfrac{5}{{13}} $ ;
The body $ C $ is balanced by the vertical components of the tension of the string. The horizontal components of tension cancel each other.
So, from the above two statements we get two equations:
 $ T\sin {\theta _1} + T'\sin {\theta _2} = 169 $ _______ $ \to eqn.1 $
 $ T\cos {\theta _1} = T'\cos {\theta _2} $ _______ $ \to eqn.2 $
Substituting the values in $ eqn.2 $ we get,
 $ \Rightarrow \dfrac{5}{{13}}T = \dfrac{{12}}{{13}}T' $
 $ \Rightarrow T = \dfrac{{12}}{5}T' $ _________ $ \to eqn.3 $
Also substituting the values in $ eqn.1 $ we get,
 $ \Rightarrow \dfrac{{12}}{{13}}T + \dfrac{5}{{13}}T' = 169 $
Now, substituting $ T $ from $ eqn.3 $ in previous equation we have,
 $ \Rightarrow (12 \times \dfrac{{12}}{5}T') + 5T' = 169 \times 13 $
 $ \Rightarrow 144T' + 25T' = 169 \times 13 \times 5 $
 $ \Rightarrow 169T' = 169 \times 13 \times 5 $
 $ \Rightarrow T' = 65kgwt $
Now putting the value of $ T' $ in $ eqn.3 $ we have:
 $ T = \dfrac{{12}}{5} \times 65kgwt = 156kgwt $
Thus, tension in shorter part of the string will be $ 65kgwt $ and in the longer part will be $ 156kgwt $ .

Note: In the given sum if instead of the unit $ kgwt $ , the magnitude of tension would have been asked to calculate the force in newton $ (N) $ then we would have used the following formula: $ T = mg $ ; where $ T $ is the tension, $ m $ is the mass of the object and $ g $ is the acceleration due to gravity. Tension in a string always balances the weight of the object suspended by the string and hence always acts along the length of the string.