Question

a and b are the angles made by a vector, from positive x and positive y axes, respectively. Which set of a and b is not possible?

\[A.\,45{}^\circ ,\,60{}^\circ \]
\[B.\,30{}^\circ ,\,60{}^\circ \]
\[C.\,60{}^\circ ,\,60{}^\circ \]
\[D.\,30{}^\circ ,\,45{}^\circ \]

Answer 1

Hint: Using the basic properties of the vectors and the direction cosines, this problem can be solved. The limits are given in the statement, like, the angles made by a vector from the positive x-axis and the positive y-axis should be taken into consideration. As the trick to solve this type of question lies in the given question statement itself.

Formula used:
\[{{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1\]

Complete step by step answer:
Consider a vector in 3D space.

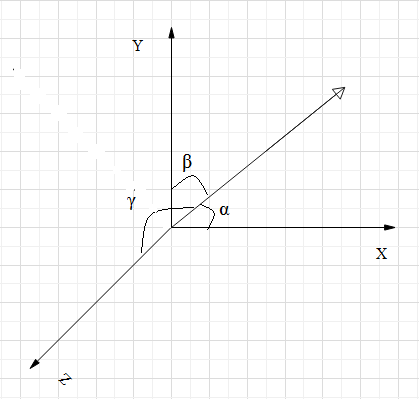
The angle made from the x-axis is called the alpha (\[\alpha \])
The angle made from the y-axis is called the beta (\[\beta \])
The angle made from the z-axis is called the gamma (\[\gamma \])
The relation between these angles made from the x-axis, y-axis and the z-axis is given as follows.
\[{{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1\]
The value of the cos angle varies between,
\[\begin{align}
  & -1<\cos \theta <1 \\
 & \Rightarrow 0<\cos \theta <1 \\
\end{align}\]
We will use hit and trial methods to solve this problem.

Consider the first option, \[A.\,45{}^\circ ,\,60{}^\circ \]
Substitute these angle values in the above equation.
So, we get,
\[\begin{align}
  & {{\cos }^{2}}45{}^\circ +{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}\gamma =1 \\
 & \Rightarrow \dfrac{1}{2}+\dfrac{1}{4}+{{\cos }^{2}}\gamma =1 \\
 & \Rightarrow {{\cos }^{2}}\gamma =\dfrac{1}{4} \\
\end{align}\]
So, this value of the angles lies between the limits of the cos function. Hence, this set of a and b is possible.

Consider the second option, \[B.\,30{}^\circ ,\,60{}^\circ \]
Substitute these angle values in the above equation.
So, we get,
\[\begin{align}
  & {{\cos }^{2}}30{}^\circ +{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}\gamma =1 \\
 & \Rightarrow \dfrac{3}{4}+\dfrac{1}{4}+{{\cos }^{2}}\gamma =1 \\
 & \Rightarrow {{\cos }^{2}}\gamma =0 \\
\end{align}\]
So, this value of the angles lies between the limits of the cos function. Hence, this set of a and b is possible.

Consider the third option, \[C.\,60{}^\circ ,\,60{}^\circ \]
Substitute these angle values in the above equation.
So, we get,
\[\begin{align}
  & {{\cos }^{2}}60{}^\circ +{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}\gamma =1 \\
 & \Rightarrow \dfrac{1}{4}+\dfrac{1}{4}+{{\cos }^{2}}\gamma =1 \\
 & \Rightarrow {{\cos }^{2}}\gamma =\dfrac{1}{2} \\
\end{align}\]
So, this value of the angles lies between the limits of the cos function. Hence, this set of a and b is possible.

Consider the fourth option, \[D.\,30{}^\circ ,\,45{}^\circ \]
Substitute these angle values in the above equation.
So, we get,
\[\begin{align}
  & {{\cos }^{2}}30{}^\circ +{{\cos }^{2}}45{}^\circ +{{\cos }^{2}}\gamma =1 \\
 & \Rightarrow \dfrac{3}{4}+\dfrac{1}{2}+{{\cos }^{2}}\gamma =1 \\
 & \Rightarrow {{\cos }^{2}}\gamma =-\dfrac{1}{4} \\
\end{align}\]
So, this value of the angles does not lie between the limits of the cos function. Hence, this set of a and b is not possible.

As the set of a and b, that is \[30{}^\circ ,\,45{}^\circ \] is not possible, thus, the option (D) is correct.

Note:
The things to be on your finger-tips for further information on solving these types of problems are: A trick to solve this type of problem is, they have given that the angles are made from the positive x-axis and positive y-axis. The angular difference between these two axes is 90 degrees, thus, the set whose angles sums less than 90 degrees do not belong to the set.