Question

A 90 degree angle triangle has one side a length of 26.1 meters, how do you find the lengths of the other sides?

Answer 1

Hint: Consider two cases according to the given question. In the first case consider the side whose length is given as the hypotenuse and try to find the other two sides. In the second case consider the side whose is given as one of the sides other than the hypotenuse and again try to find the remaining two sides.

Complete step-by-step solution:
Here we have been provided with a right angle triangle with the length of one of its sides as 26.1 meters. We have been asked to determine the length of the remaining two sides. Since, we don’t know which side length is given to us so we need to consider two cases.
(1) In this case we will consider the side length of 26.1 meters as the hypotenuse.

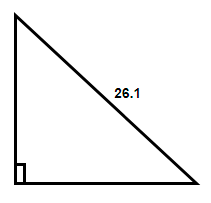
Now, from the above figure we need to determine the length of the base and the perpendicular. Here we will need at least one more angle so that we can use the formulas of the trigonometry to determine the sides. Therefore, we cannot determine the length of the other two sides here.
(2) In this case we will consider the side length of 26.1 meters as either the base or the perpendicular.

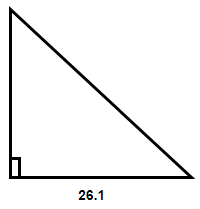
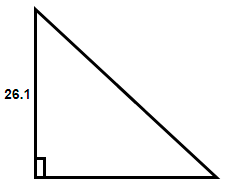
Now, from the above figures we need to determine the length of the hypotenuse and the other side. Here also we will need at least one more angle so that we can use the formulas of the trigonometry to determine the sides. Therefore, here also we cannot determine the length of the other two unknown sides.

Note: You may note that we must be provided with at least two angles and a side or two sides and one angle with two sides to determine the other unknown values of the triangle. In the above question we were provided with one angle and one side only and that is why we were not able to find the length of the other two sides.