Question

A 25 kg uniform solid sphere with a 20 cm radius is suspended by a vertical wire such that the point of suspension is vertically above the centre of the sphere. A torque of 0.10 N-m is required to rotate the sphere through an angle of 1.0 rad and then maintain the orientation. if the sphere is then released, its time period of the oscillation will be
A. $\pi $second
B. $\sqrt 2 \pi $ second
C. $2\pi $ second
D. $4\pi $ second

Answer 1

Hint: In case of simple harmonic motion there will be a mean position and two extreme positions. The particle executes the SHM with respect to the mean position and within the range of two extreme positions. Generally simple harmonic motions are denoted with the sinusoidal or cosecant functions.

Formula used:
$x = A\sin (\omega t)$

Complete step-by-step answer:
In SHM acceleration of the particle executing the SHM is proportional to the displacement of the particle from the mean position. Generally if an object starts from the mean position then we write displacement as a sinusoidal function and if an object starts from the extreme position then we write the displacement of a body as a cosine function. We can assume in any way if it is not specified in the question. Let us assume that the given particle is executing the SHM about the mean position. Then the function of the SHM displacement will be $x = A\sin (\varphi )$ where $\varphi $ is the phase of the particle. That phase will be generally given as $\varphi = \omega t$ and A is the amplitude and $\omega = 2\pi f$ is the angular velocity and $f$ is the frequency.
So the displacement equation will become
$x = A\sin (\omega t)$
And the acceleration will be
$a = - {\omega ^2}x$
In terms of rotation, it can also be written as
$\alpha = - {\omega ^2}\theta $
That means linear acceleration is replaced by angular acceleration alpha and linear displacement got replaced by angular displacement theta. Diagram is given below for clear understanding and it represents the given system of solid sphere and wire.

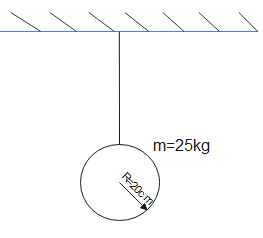
From the information given we have
Torque required per unit twist i.e for rotation of one radian is
$\eqalign{
  & k = \dfrac{{0.1}}{1} \cr
  & \therefore k = 0.1 \cr} $
Moment of inertia is I.
$\eqalign{
  & I = \dfrac{2}{5}m{r^2} \cr
  & \Rightarrow I = \dfrac{2}{5}\left( {25} \right){\left( {20 \times {{10}^{ - 2}}} \right)^2} \cr
  & \therefore I = 0.4kg - {m^2} \cr} $
Time period is given as T
$\eqalign{
  & I\alpha = - k\theta \cr
  & \Rightarrow T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{I}{k}} \cr
  & \Rightarrow T = 2\pi \sqrt {\dfrac{{0.4}}{{0.1}}} \cr
  & \therefore T = 4\pi \cr} $
Hence option D will be the answer.

So, the correct answer is “Option D”.

Note: In the question they had asked to find out the time period of oscillatory motion of sphere. Actually simple harmonic motion and oscillatory motion are not the same. Even though in both cases force is opposite to the displacement, in SHM force is proportional to linear power of displacement while in oscillatory motion it is proportional to any odd powers of displacement. Here we assumed it is SHM to find out the time period.