Question

A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.

Answer 1

Hint: Find the volume of well by using \[{{V}_{C}}=\pi {{r}^{2}}h\] and find the volume of the platform by using \[{{V}_{d}}=L\times B\times H\]. Then we know that the volume will remain constant, so equate the volume of the well and platform to get the height of the platform.

Complete step by step solution:
Here, we are given that a 20m deep well with diameter 7m is dug and the earth from digging it is evenly spread out to form a platform 22m by 14m. We have to find the height of this platform.
Before proceeding with the question, we must know that when one object of a particular shape is converted into other object/objects of the same or different shape, then volume always remains constant. That is, the volume of the object before and after the conversion would be the same. While the other quantities such as surface area, length, breadth, radius, etc. could change.
Now we know that well is cylindrical and earth from digging it is spread to form a platform of cuboidal shape. So, indirectly we can say that the cylindrical shape of the well is converted into the cuboidal shape of the platform, so the volume will remain constant. We can consider the figure as below,

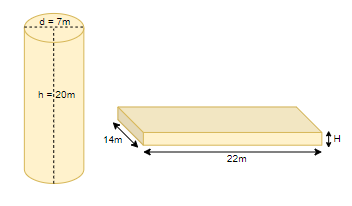
We know that volume of the cylinder \[\left( {{V}_{C}} \right)=\pi {{r}^{2}}h\] where r is the radius of cylinder and h is the height of the cylinder. We are given that \[\text{radius = }\left( \dfrac{\text{Diameter}}{2} \right)\] of well is \[\dfrac{7}{2}=3.5m\] and the height of the well is 20 m. By substituting the values of r and h in the equation of volume of cylinder, we get
The volume of a cylindrical well \[=\pi {{\left( \dfrac{7}{2} \right)}^{2}}\left( 20 \right)\]
\[\begin{align}
  & =\pi \times \dfrac{49}{4}\times 20 \\
 & =245\pi \text{ c}{{\text{m}}^{3}} \\
\end{align}\]
We also know that volume of cuboid \[\left( {{V}_{D}} \right)=L\times B\times H\] where L, B and H are the length, breadth and height of the cuboid respectively. We are given that L = 22m and B = 14m for the platform. By substituting these values in the volume of a cuboid, we get,
The volume of cuboidal platform \[=22\times 14\times H=308\times H\text{ c}{{\text{m}}^{3}}\]
Now, we know that volume of well is equal to the volume of the platform. So, we get,
The volume of cylindrical well = Volume of cuboidal platform. By substituting the values of LHS and RHS, we get,
\[245\pi =308\times H\]
By substituting \[\pi =\dfrac{22}{7}\], we get,
\[245\times \dfrac{22}{7}=308\times H\]
By dividing by 308 on both sides, we get
\[\Rightarrow H=\dfrac{245\times 22}{7\times 308}\]
\[\Rightarrow H=\dfrac{5}{2}=2.5m\]
So, we get the height of the platform as 2.5m.

Note: Students often make this mistake of using the formulas of volume, area, etc. without properly looking whether the radius or diameter is given in the question. They must properly read and if the diameter is given, first convert it into radius and then only put it into the formula to get the desired value. Also, students must remember that whenever any 3-dimensional object is converted into another, then volume always remains constant.