Question

A 1.5 m tall boy standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

Answer 1

Use the tangent formula \[\tan \theta = \dfrac{{{\text{Opposite Side}}}}{{{\text{Adjacent Side}}}}\] to find the distance of the boy from the building at angle of elevation 30° and 60° and find the difference between them to find the distance he walked. Let the distance b/w boy at 60° and building is y and distance travelled by boy from starting point to 60° angle point is x.

Complete step-by-step solution -

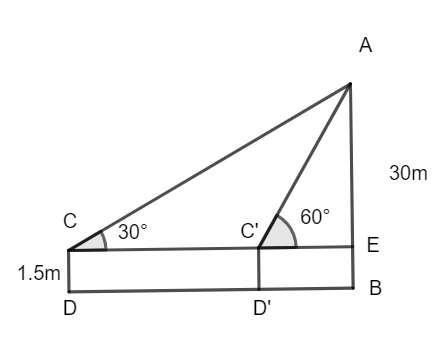
In the figure, AB is the building of height 30 m and CD is the boy 1.5 m tall. The parallel line to the ground passing through C meets AB at E.
AE = AB – BE
AE = 30 – 1.5
AE = 28.5 m
Angle of elevation is the angle between the line of sight of the observer and the horizontal.

We know that the formula for tangent of an angle is given as follows:
\[\tan \theta = \dfrac{{{\text{Opposite Side}}}}{{{\text{Adjacent Side}}}}\]
In triangle ACE, we have the angle of elevation as 30°, then, we have:
\[\tan 30^\circ = \dfrac{{{\text{28}}{\text{.5}}}}{{x + y}}\]
We know that the value of \[\tan 30^\circ \] is \[\dfrac{1}{{\sqrt 3 }}\], hence, we have:
\[\dfrac{1}{{\sqrt 3 }} = \dfrac{{{\text{28}}{\text{.5}}}}{{x + y}}\]
Simplifying, we have:
\[x + y = {\text{28}}{\text{.5}}\sqrt 3 ............(1)\]
Now, In triangle AC’E, we have the angle of elevation as 60°, then, we have:
\[\tan 60^\circ = \dfrac{{{\text{28}}{\text{.5}}}}{y}\]
We know that the value of \[\tan 60^\circ \] is \[\sqrt 3 \], hence, we have:
\[\sqrt 3 = \dfrac{{{\text{28}}{\text{.5}}}}{y}\]
Simplifying, we have:
\[y = \dfrac{{{\text{28}}{\text{.5}}}}{{\sqrt 3 }}\]
\[y = \dfrac{{{\text{28}}{\text{.5}}}}{3} \times \sqrt 3 \]
\[y = 9.5\sqrt 3 ..............(2)\]
Using equation (2) in equation (1),
\[x + 9.{\text{5}}\sqrt 3 = {\text{28}}{\text{.5}}\sqrt 3 \]
Solving for x, we have:
\[x = {\text{28}}{\text{.5}}\sqrt 3 - 9.{\text{5}}\sqrt 3 \]
\[x = {\text{19}}\sqrt 3 m\]
Hence, the distance the boy travelled is \[{\text{19}}\sqrt 3 \] m.

Note: Do not use the height of the building 30 m in the tangent formula, the angle of elevation is from 1.5 m above the ground. Hence, account for the height of the boy, otherwise the answer will be wrong.