Question

A $1.2m$ tall girl spotted a balloon moving with wind in a horizontal line at a height of $88.2m$ from the ground. The angle of elevation of the balloon from the eyes of the girl at any point instant is ${{60}^{\circ }}$ . After sometime, the angle of elevation reduces to ${{30}^{\circ }}$ . Find the distance travelled by the balloon during the interval.

Answer 1

Hint: We can answer this question by applying the concept of trigonometric ratios in the respective angles using the formulae $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$ and the values of the specified angles as $\tan {{60}^{\circ }}=\sqrt{3}$ and $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ . After further simplifying we will come to the conclusion of the value.

Complete step by step answer:
Now considering from the question we have been given that a $1.2m$ tall girl spots a balloon moving with wind in a horizontal line at a height of $88.2m$ from the ground. The angle of elevation of the balloon from the eyes of the girl at any point instant is ${{60}^{\circ }}$ . After sometime, the angle of elevation reduces to ${{30}^{\circ }}$ .
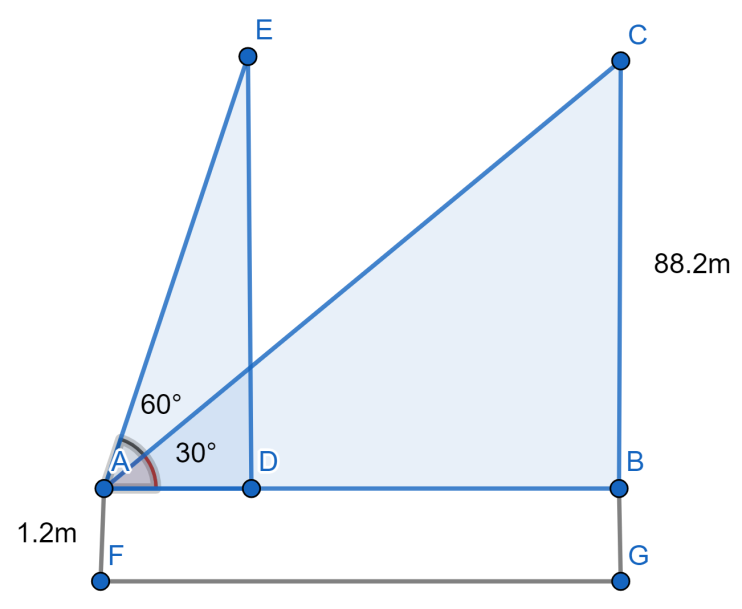
Let us illustrate this with a figure here $AF=1.2m$ and $CG=88.2m$ as $CB$ is parallel to $ED$ and as it is given that the angles are $\angle CAB={{30}^{\circ }}$ and $\angle CAE={{60}^{\circ }}$. Let us assume $AD=x$ and $BD=y$ .
The distance travelled by the balloon during the interval is $BD=y$ .

As we know that $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$ .
As we know that by applying tangent of angles we will have $\tan {{60}^{\circ }}=\dfrac{DE}{DA}=\dfrac{88.2-1.2}{x}$ and $\tan {{30}^{\circ }}=\dfrac{CB}{AB}=\dfrac{88.2-1.2}{x+y}$ .
From the specified values of the trigonometric ratios we know that $\tan {{60}^{\circ }}=\sqrt{3}$ and$\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ .
By using these values in the above expressions we can say that $\dfrac{87}{x}=\sqrt{3}$ from that we will have $x=\dfrac{87}{\sqrt{3}}$ .
By using these values in the above expressions we can say that $\dfrac{87}{x+y}=\dfrac{1}{\sqrt{3}}$ from that we will have $x+y=87\sqrt{3}$ .
By using this value of $x$ in the other expression we will have $\dfrac{87}{\sqrt{3}}+y=87\sqrt{3}$ .
By further solving this we will have
$\begin{align}
  & y=87\sqrt{3}-\dfrac{87}{\sqrt{3}} \\
 & \Rightarrow y=87\left( \sqrt{3}-\dfrac{1}{\sqrt{3}} \right) \\
 & \Rightarrow y=87\left( \dfrac{3-1}{\sqrt{3}} \right) \\
 & \Rightarrow y=\dfrac{87\times 2}{\sqrt{3}} \\
 & \Rightarrow y=58\sqrt{3} \\
\end{align}$
Hence we can conclude that the distance travelled by the balloon during the interval is $58\sqrt{3}=100.45m$ .

Note:
We should be sure with the calculations that we perform and clear with the concepts of trigonometric that we are going to apply. If in case by mistake we had interchanged the values of the specified angles or if we had made a calculation mistake or if we had forgotten to subtract the height of the girl from the length of the height at which the balloon is located cases like these will yield us wrong conclusions.