Question

8 girls shared \[\dfrac{4}{5}\] of cake equally. What fraction of the cake did each girl receive?

Answer 1

Hint: Here there are eight girls, we are asked to find the part of the cake that each girl received on sharing a \[\dfrac{4}{5}\] part of cake equally among them. Since it is given that a \[\dfrac{4}{5}\] part of the cake is equally shared among eight girls then the part that each girl received will be found by dividing the part of the cake into eight.

Complete step-by-step solution:
It is given that a \[\dfrac{4}{5}\] part of the cake is shared equally among eight girls. We aim to find the part of the cake that each girl received.
Let us imagine a \[\dfrac{4}{5}\] part of the cake.

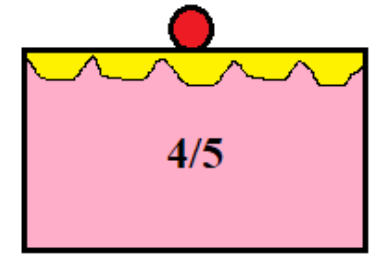
Now, this part of a cake is equally cut into eight parts to distribute among eight girls.

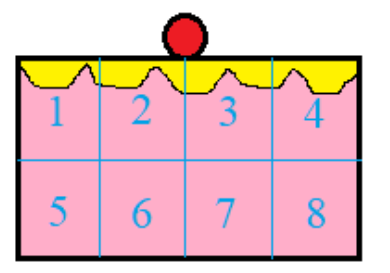
Now we have to find the fraction of each part.
We can see that a \[\dfrac{4}{5}\] part of the cake is divided into eight equal parts. That is \[\dfrac{4}{5} \div 8\]. Now on dividing this we get each fraction part.
We know that we cannot do direct division on fractions, we have to reciprocal the divisor and multiply it to the dividend (fraction). On doing this we get
\[\dfrac{4}{5} \div 8 = \dfrac{4}{5} \times \dfrac{1}{8}\] where \[\dfrac{1}{8}\] is the reciprocal of the divisor \[8\]
Now let us simplify this to get the required value. On canceling four on the numerator and eight on the denominator we get
\[\dfrac{4}{5} \times \dfrac{1}{8} = \dfrac{1}{5} \times \dfrac{1}{2}\]
On further simplification, we get
\[\dfrac{1}{5} \times \dfrac{1}{2} = \dfrac{1}{{10}}\]
Thus, we have found the value of \[\dfrac{4}{5} \div 8\] that is \[\dfrac{1}{{10}}\].
Therefore, \[\dfrac{4}{5}\] part of the cake is divided into eight equal parts of fraction \[\dfrac{1}{{10}}\] each.
Let us draw a diagram for a clear idea.

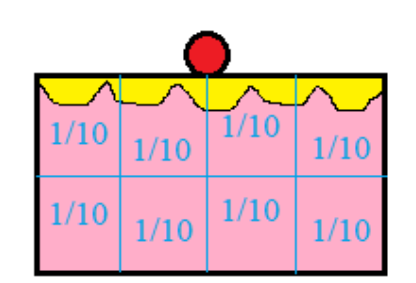
We can also check whether we got the correct answer or not. We have found that the fraction of each part is \[\dfrac{1}{{10}}\]. if we add all eight fraction parts (i.e., \[\dfrac{1}{{10}}\]) we have to get the whole part of a cake (i.e., \[\dfrac{4}{5}\]).
That is \[\dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} + \dfrac{1}{{10}} = \dfrac{4}{5}\]
Let us verify this. On simplifying the left-hand side, we get
\[\dfrac{1}{{10}} \times 8 = \dfrac{4}{5}\]
\[\dfrac{8}{{10}} = \dfrac{4}{5}\]
On canceling eight on the numerator and ten on the denominator we get
\[\dfrac{4}{5} = \dfrac{4}{5}\]
Thus, we have verified that L.H.S equal to R.H.S
Therefore, the value that we calculated above is correct.

Note: Division is nothing but dividing a whole part equally by the required number. Here we are provided with the whole part of a cake and the number by which it has to be divided so, we divide the given whole part of a cake by eight which will give us the fraction part of each piece of cake.