Question

How many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7, and 9 when no digit is repeated? How many of them are divisible by 10?

Answer 1

Hint: For the lakh’s place, we have to any digit from 1,3,5,7,9. So, for lakh’s place, we have 5 digits. For ten-thousands place, we can take any digit but not that digit which is taken for lakh’s place because repetition is not allowed. As zero is not taken for the lakh’s place but it can be included for the ten-thousands place. So, there are 5 intakes for the ten-thousands place. As repetition is not allowed we have only 4 intakes for thousand’s place. Similarly, we have 3,2 and 1 intakes for hundred’s, ten’s and one’s place. Total numbers that can be formed \[=5\times 5\times 4\times 3\times 2\times 1=600\]. A number to be divisible by 10 should have 0 at one’s place. So, fix 0 at the one’s place and then find the intakes for lakhs, ten-thousands, thousands, hundred’s and ten’s place that are 5,4,3, and 2. Hence, the total numbers are \[5\times 4\times 3\times 2=120\] .

Complete step-by-step answer:
Now, we have to find the number of 6 digit numbers. For that, we have to find the number of possibilities of digits at lakhs place, ten-thousands place, thousand’s place, hundred’s place, ten’s place, and one’s place.
For lakh places, we can choose any digit from 1,3,5,7, and 9. We have 5 possibilities for this.
For a ten-thousand place, 0 should also be included as a possibility. We have 5 digits possible because repetition is not allowed.
For the thousand’s place, we have 4 digits left allowing there to be no repetition.
Similarly, for hundred’s, ten’s and one’s place we have 3,2 and 1 digit possible. Let us understand with a diagram.

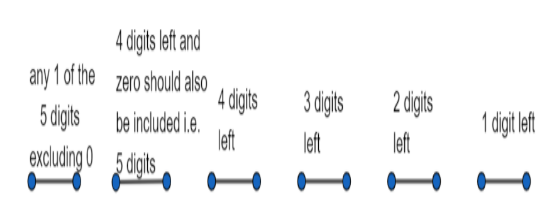
The total number of 6 digit numbers \[=5\times 5\times 4\times 3\times 2\times 1=600\] .
To find the numbers which are divisible by 10, we should have 0 at the one’s place.
Now for lakhs place, we have to choose digits from 1,3,5,7, and 9. It means we have 5 digits possible.
For a ten-thousand place, we have 4 digits left because there should not be repetition. Similarly, we have 3,2 and 1 digit possible for thousand’s, hundreds, and tens place respectively.

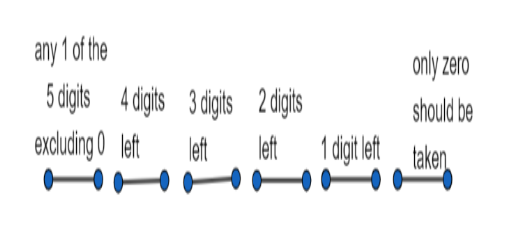
The total number of 6 digit numbers that are divisible by 10 \[=5\times 4\times 3\times 2\times 1\times 1=120\] .

Note: In this question, the common mistake that can be done is taking “0” at the lakh’s place. As numbers consist of any digit from 0 to 9. But we cannot take 0 at lakh’s place. If we do so then our number will be a five-digit number. But we have to form a 6-digit number. So, we have to ignore “0” to be included in lakh’s place.