Question

20 teachers of a school teach either mathematics or physics. 12 of them teach mathematics while 4 teach both the subjects. Then number of teacher teaching only physics is
(a) 12
(b) 8
(c) 6
(d) None of these

Answer 1

Hint: To solve this problem we will first draw the venn diagram of the given problem using the data mentioned to understand the problem more clearly. Then we will apply the formula $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$ where A is set of mathematics teachers and B is the set of physics teachers. After putting the required values in this formula we will get the value of n(B) and that will be our answer.

Complete step by step answer:
We are given that there are total 20 teachers in a school, out of which 12 teaches mathematics and 4 teaches both mathematics and physics,
And we have to find the number of teachers who teaches physics only,
So first of all we will try to present this problem diagrammatically by drawing the venn diagram of the given data as,

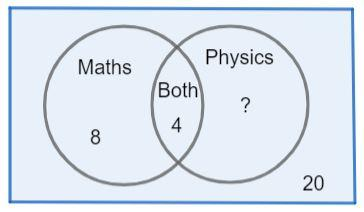
Now if we assume,
A = set of teachers who teaches mathematics
B = set of teachers who teaches Physics
Then according to the question we have,
$n\left( A \right)=12$ and,
$n\left( A\cup B \right)=20$
$n\left( A\bigcap B \right)=4$
And we know that,
$n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$
Now putting the above mentioned values in this equation, we get
$\begin{align}
  & 20=12+n\left( B \right)-4 \\
 & 20-12=n\left( B \right)-4 \\
 & 8=n\left( B \right)-4 \\
 & n\left( B \right)=8+4 \\
 & n\left( B \right)=12 \\
\end{align}$
Now we got the number of teachers who teaches physics as 12, but this also includes those teachers who teaches maths also so we have to subtract those teachers who teaches both subjects from this,
So we get,
Number of teachers teaching only physics = total number of teachers who teaches physics – number of teachers who teaches both.
Hence,
Number of teachers teaching only physics = 12 – 4 = 8

So, the correct answer is “Option B”.

Note: To solve problems related to sets or which involve union or intersection data try to draw a venn diagram for that problem. And also many students here may directly write the answer as n(B) = 12, but that will be wrong as we are asked to find teachers who teach physics only and not the total number of teachers who teach physics, so be careful about that.