Question

1.What is the equation of the circle in general form \[?\]

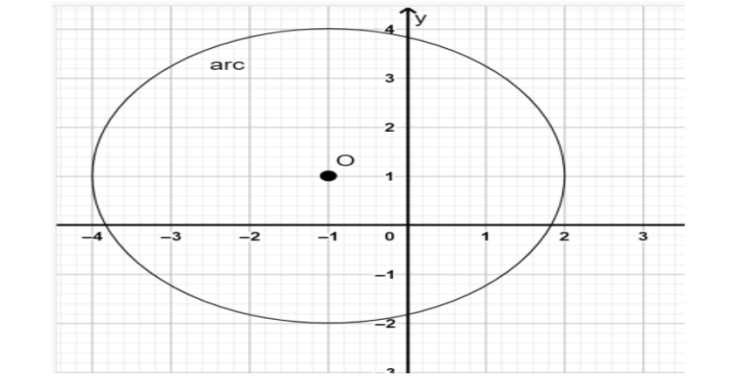
2. Write the equation of circle in general form. Show your work for the above graph.

Answer 1

Hint: We have to find the equation of the given circle. So, first we have to find the centre of the given circle and then find the radius of the given circle. Then using the equation of the circle in general form, find the equation of the given circle.

Complete step-by-step answer:
1.Equation of a circle when the centre is not an Origin: Let \[C(a,b)\] be the centre of the circle and
 \[p(x,y)\] be any point on the circle, the radius of a circle is ‘ \[r\] ’. Then the equation of the circle with centre \[\left( {a,b} \right)\] and the radius of a circle \[r\] is given by
 \[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}\] ---(1)
The equation (1) is known as the general equation of the circle.
Equation of a circle when the centre is an Origin: Let \[p(x,y)\] be any arbitrary point on the circle. Let \[r\] be the radius of a circle and with the centre at the origin. Then equation of the circle is given by
 \[{x^2} + {y^2} = {r^2}\] --(2)

2.In the given circle \[( - 1,1)\] is the centre of the circle. Since the point \[\left( {2,1} \right)\] is on the circle. Then radius is equal to distance between any point on the circle and the centre of the circle.
Hence \[r = \sqrt {{{(2 - ( - 1))}^2} + {{(1 - 1)}^2}} = 3units\]
 Then the equation of the given circle is \[{\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = 9\] .

Note: A circle is formed when an arc is drawn from the fixed point called the centre (an arc rotating from a fixed point until it reaches the initial point after complete rotation), in which all the points on the curve are having the same distance from the centre point of the centre.