Question

When $0.2M$ acetic acid is neutralized with $0.1M$ NaOH in $0.5$ liters of water, the resultant solution is slightly alkaline. Calculate the pH of the resulting solution given that ${K_a}$ for $C{H_3}COOH = 1.8 \times {10^{ - 5}}$

Answer 1

Hint:The reaction between acetic acid and sodium hydroxide produces sodium acetate and water. Calculate the amount of sodium acetate and water produced in this reaction and find the concentration of sodium acetate accordingly. Now calculate the value of hydrolysis constant or ${K_h}$ to find the pH value.

Complete step-by-step solution:The above reaction between acetic acid and sodium hydroxide can be written as follows.
$C{H_3}COOH + NaOH \rightleftarrows C{H_3}COONa + {H_2}O$
$0.2M$ of acetic acid would give $0.2M$ of sodium acetate and $0.5$ liters of water. So the concentration of sodium acetate would be $0.1mol{L^{ - 1}}$
Given to us the association constant of acetic acid as ${K_a} = 1.8 \times {10^{ - 5}}$
Let us write the association reaction for acetic acid $C{H_3}CO{O^ - } + {H_2}O \rightleftarrows C{H_3}COOH + O{H^ - }$
For the above equilibrium reaction, we can write the concentrations as:

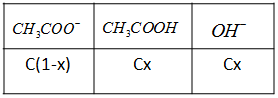
From this, we can write the value of hydrolysis constant as ${K_h} = \dfrac{{Cx \times Cx}}{{C\left( {1 - x} \right)}} = \dfrac{{C{x^2}}}{{1 - x}}$
Since the value of x is extremely small, we can approximate the value of $1 - x$ to be $1$ and hence the equation becomes ${K_h} = C{x^2}$
Now, we know that ${K_h} = \dfrac{{{K_w}}}{{{K_a}}}$ where ${K_w} = {10^{ - 14}}$ and the ${K_a}$ value is already given. By substituting these values, we get ${K_h} = \dfrac{{{{10}^{ - 14}}}}{{1.8 \times {{10}^{ - 5}}}} = 0.55 \times {10^{ - 9}}$
From this, we can write $C{x^2} = 0.55 \times {10^{ - 9}}$
We have already calculated the concentration as $0.1mol{L^{ - 1}}$ and by substituting this, we get ${x^2} = 5.5 \times {10^{ - 9}}$
This gives $x = 7.42 \times {10^{ - 5}}$
From the above table, the concentration of $O{H^ - }$ is $Cx = 0.1 \times 7.42 \times {10^{ - 5}} = 7.42 \times {10^{ - 6}}$
We know that the product of concentration of ${H^ + }$ and $O{H^ - }$ of a solution gives the value of dissociation constant of water.
$\left[ {{H^ + }} \right]\left[ {O{H^ - }} \right] = {K_w}$
From this, we can calculate the concentration of ${H^ + }$ as $\left[ {{H^ + }} \right] = \dfrac{{{K_w}}}{{\left[ {O{H^ - }} \right]}} = \dfrac{{{{10}^{ - 14}}}}{{7.42 \times {{10}^{ - 6}}}} = 1.347 \times {10^{ - 9}}M$
Now we can calculate the pH value as $ - \log \left[ {{H^ + }} \right] = 8.87$
Hence the pH value is $8.87$

Note: It is to be noted that we can also find the value of pOH first and derive the value of pH. This is because of the relation $pH + pOH = 14$ and hence the value of pH can be calculated. Therefore the pOH of this solution would be $14 - pH$ which is $14 - 8.87 = 5.13$ .