What is Volume?
The quantity that is used to calculate how much space there is inside a cuboid is called its volume. A cuboid is a common three-dimensional shape that surrounds us that is a room. Based on a shape's parameters, such as its length, breadth, and height, the term "volume" is used to describe how much space of that shape is contained. A formula particular to a cuboid's shape will be used to determine the volume of a cuboid.
What is the Formula for the Volume of a Cuboid?
In general, the volume of a cuboid is equal to the area that it takes up in space. It is dependent upon the cuboid's three dimensions, or its length, breadth, and height. All of the angles and the opposite faces of a cuboid in a rectangular cuboid are at right angles. Because the cuboid's volume depends on its length, breadth, and height, changing any one of those measurements alters the volume of the shape. Cuboid's volume is expressed as the \[{(unit)^3}\].
The idea described on rectangular sheets can be used to get the formula for the cuboid's volume. Let A stand for the area of a rectangular piece of paper, h for the height at which they are stacked, and V for the cuboid's volume. The cuboid's volume is then calculated by multiplying its base area by its height.
Cuboid volume equals base area minus height.
The cuboid's base area is equal to \[l \times b\].
Consequently, a cuboid's volume is given by \[V = l \times b \times h\].
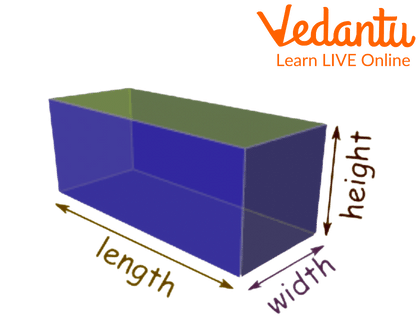
Cuboid
Volume of Cuboid Formula
A cuboid's volume is determined by the product of its length, breadth, and height. Cubic units, often known as \[{(unit)^3}\], include \[{m^3},c{m^3}\], etc. as the unit of volume for cuboids.
The product of a cuboid's base area and height determines its volume. We can therefore write:
Cuboid volume equals base area times height (in cubic units).
The cuboid's base is shaped like a rectangle. As a result, a cuboid's base area is determined by multiplying its length by its breadth. Hence, A cuboid's volume is equal to the multiplication of length, breadth, and height in cubic units.
How to Find Volume of Cuboid
Using the cuboid volume formula, the volume of the cuboid can be determined. To determine a cuboid's volume, follow these steps:
Step 1: Verify whether or not the cuboids' specified dimensions are in the same units. In that case, if the units are not the same, then change the dimensions to match the units.
Step 2: Multiply the cuboid's length, breadth, and height once the dimensions are all expressed in the same units.
Step 3: After you've calculated the value, write the unit at the end.
Conclusion
A cuboid's volume is the amount of space it occupies in three dimensions. A cuboid is a three-dimensional shape having six rectangular faces. Two pairs of three parallel faces make up each of these six cuboid faces. The volume of a cuboid is measured in cubic units.
The Volume of Cuboid Examples
Example 1: Calculate the volume of a cuboid with dimensions of 7 inches long, 5 inches wide, and 2 inches high.
Ans: As is well known, \[V = l \times b \times h\] for a cuboid's volume.
Here, the dimensions are as follows: \[l = 7 inches, b = 5inches, h = 2 inches\].
The volume of the cuboid is therefore \[V = l \times b \times h\].
\[V = 7 \times 5 \times 2\]
\[V = 70\, inche{s^3}\]
The cuboid has a volume of \[70\,inche{s^3}\].
Example 2: If a cuboidal fish aquarium has the following measurements: 30 inches, 20 inches, and 15 inches. Can you estimate the size of the fish tank?
Fish Aquarium
Ans: The fish aquarium is, as we all know, shaped like a cube. Consequently, the fish tank's measurements are as follows:
The aquarium is 30 inches long.
The aquarium is 20 inches wide.
The aquarium is 15 inches tall.
The aquarium's volume is calculated as follows:
\[V = l \times b \times h\]
\[V = 30 \times 20 \times 15\]
\[V = 9000\]
The cuboidal fish tank has a \[9000\, inc{h^3}\] volume.
Example 3: Determine how much air may be accumulated in a space that is 5 inches long, 6 inches wide, and 10 inches high.
Ans: Capacity of a room = volume of a cuboid = maximum amount of air that can be gathered in space.
\[\begin{array}{l}V = 5 \times 6 \times 10\\V = 300\\V = 300 inc{h^3}\end{array}\]
Thus, this space can hold up to \[300 inc{h^3}\] of air at a time.
FAQs on What is the Formula of the Volume of a Cuboid?
1. Does the cuboid order affect how much volume is calculated?
Ans: A cuboid can be kept either vertically or horizontally; it makes no difference. Even if the cuboid's length, width, and height are arranged differently, its volume remains the same.
2. Who made the discovery of volume?
Ans: Early in the 17th century, Bonaventura Cavalieri used the principles of contemporary integral calculus to determine an object's volume.
3. How does halving the side length affect the cuboid's volume?
Ans: The cuboid's volume is cut in half as soon as its length is cut in half as the volume of the cuboid is directly proportional to its length. Thus, as soon as we halve the length of the cuboid, its volume will also be halved.
