




Key Differences Between Corresponding and Alternate Angles
Corresponding and Alternate angles are the most fundamental angles formed when two parallel lines are intersected by a transversal line. In this article, we will discuss the Corresponding and Alternate Angle Theorems in detail along with their proof in detail. Corresponding and Alternate Angles are the most widely used tool in Geometry. Parallel lines find many applications in our day-to-day life and so do the properties of parallel lines such as corresponding and alternate angles. Corresponding and Alternate Angles theorems form a fundamental tool of Euclidean Geometry.
Statement of Corresponding and Alternate Angle Theorems
Alternate Angle Theorem
The theorem states that if a line referred to as transversal intersects parallel lines, the alternate interior angles are congruent.
Corresponding Angle Theorem
The theorem states that if a transversal intersects parallel lines, the corresponding angles are congruent.
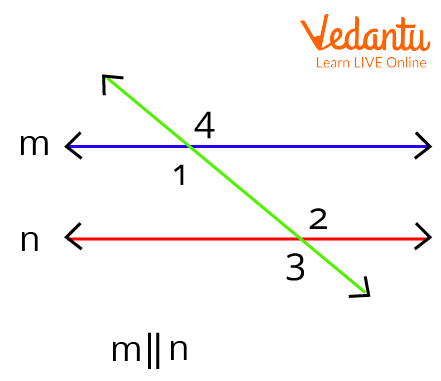
Angles made by two parallel lines m and n
In the above diagram, these $\angle 1=\angle 3, \angle 2=\angle 4$ are the corresponding angles, and $\angle 1=\angle 2$ are alternate interior angles.
Proof of Corresponding and Alternate Theorems
Alternate Angles Theorem
Given: Lines $p\parallel q$
To prove: $\angle 2 = \angle 7$ and $\angle 3 = \angle 6$
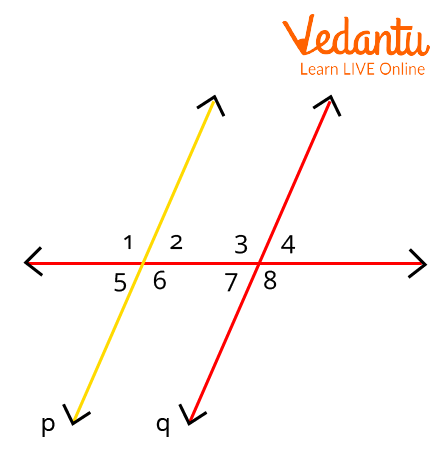
Proof of Alternate Angle Theorem
Proof: Let us assume that $p$ and $q$ are two parallel lines and $t$ is the transversal that intersects parallel lines $p$ and $q$. We know that if a transversal intersects any two parallel lines, the corresponding angles and vertically opposite angles are equal.
Therefore,
$\Rightarrow \angle 1 = \angle 3 \quad \ldots$ (i) (Corresponding angles)
$\Rightarrow \angle 1 = \angle 6$....(ii) (Vertically opposite angles)
From equations (i) and (ii), we get
$\Rightarrow \angle 3 = \angle 6 \quad$ (Alternate interior angles)
Similarly,
$\Rightarrow \angle 2 = \angle 7$
Hence, the proof of the Alternate Angle Theorem.
Corresponding Angles Theorem
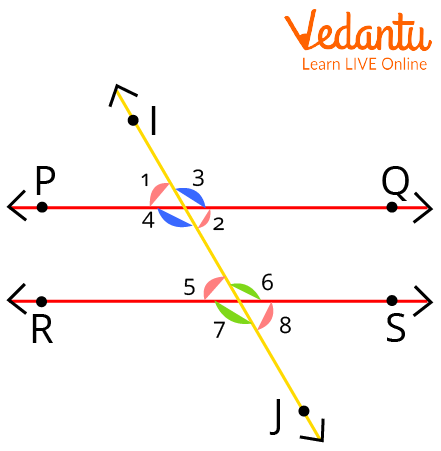
Proof of Corresponding angle Theorem
To Prove:
$\angle 1 = \angle 5,\angle 3 = \angle 6,\angle 4 = \angle 7,\angle 2 = \angle 8$
Given, PQ and RS are the two parallel lines intersected by the transversal IJ.
Now, if $PQ\parallel RS$, then by the corresponding angles theorem, we can write
$\angle 1 = \angle 5$
$\angle 3 = \angle 6$
$\angle 4 = \angle 7$
$\angle 2 = \angle 8$
Remember: The theorem can only be proved when parallel lines are given.
Thus, this theorem is true without proof.
Limitations of Corresponding and Alternate Angle Theorems
Both the theorems are applicable only if transversal lines intersect the parallel lines.
They are not applicable in the case of nonparallel lines as the nonparallel lines do not form corresponding and alternate angles.
Applications of Corresponding and Alternate Angle Theorems
Both Theorems are applicable in geometry to solve questions related to corresponding angles and alternate angles.
Rubik's Cube, railway tracks, and opening and shutting of geometry boxes are examples of corresponding angles.
Solved Examples
1. Find the value of angle $x$ in the given figure if the two lines are parallel and they are crossed by a transversal.
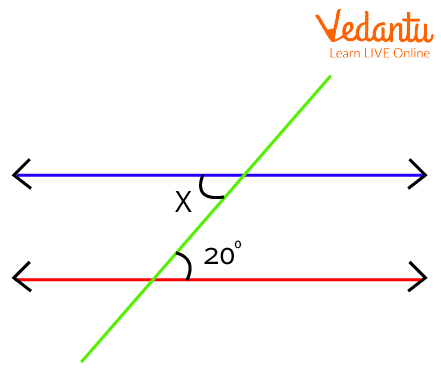
Given figure to find angle x
Ans:
By the alternate interior angles theorem,
$x$ and $20^{\circ}$ are the alternate interior angles. Hence, they are equal.
Therefore,
$\Rightarrow x = 20^{\circ}$.
2. The two corresponding angles are given to be $9 x+10$ and 64. What is the value of $x$?
Ans: The two given corresponding angles are congruent.
$9 x+10= 64 \\$
$\Rightarrow 9 x=64-10 \\$
$\Rightarrow 9 x=54 \\$
$\Rightarrow x=6$
3. The values of two corresponding angles $\angle 2=5 x+6$ and $\angle 6=3 x+18$. Solve for the value of $x$.
Ans: As they are corresponding angles and the lines are said to be parallel in nature, then they should be congruent.
Equate the given expressions $\angle 2=5 x+2$ and $\angle 6=3 x+10$ and find the value of $x$.
$5 x+6=3 x+18$
$\Rightarrow 5 x-3 x=18-6$
$\Rightarrow 2 x=12$
$\Rightarrow x=\dfrac{12}{2}$
$\Rightarrow x=6$
Important Formulas to Remember
Corresponding angles theorem: If two parallel lines are intersected by transversal lines, then the corresponding angles are equal.
Alternate angles theorem: If two parallel lines are intersected by transversal lines, then alternate angles are equal.
Important Points to Remember
Corresponding Angles are formed on the same side of parallel lines intersected by a transversal line.
Alternate angles are formed on opposite sides of parallel lines intersected by a transversal line.
Conclusion
In the article, we have discussed the detailed proof of Corresponding and Alternate Angle Theorems and the applications of the corresponding and alternate angles. These theorems are fundamental tools in geometry and form the basis of angle theory. These theorems are of great importance and so are necessary to be studied.
FAQs on Corresponding and Alternate Angle Theorem Made Simple
1. What is the definition of corresponding angles in geometry?
Corresponding angles are pairs of angles that are in the same relative position at each intersection where a straight line, called a transversal, crosses two other lines. If the two lines are parallel, then the corresponding angles are equal. For example, the angle in the top-left corner of one intersection will correspond to the angle in the top-left corner of the other intersection.
2. What are the different types of alternate angles?
Alternate angles are formed on opposite sides of the transversal. They are categorised into two main types based on their position relative to the two lines the transversal intersects:
Alternate Interior Angles: These are a pair of angles on opposite sides of the transversal but inside the two lines. They form a 'Z' or 'S' shape.
Alternate Exterior Angles: These are a pair of angles on opposite sides of the transversal but outside the two lines.
According to the theorem, these pairs of angles are equal if the two lines cut by the transversal are parallel.
3. What is the main difference between corresponding angles and alternate angles?
The main difference lies in their position relative to the transversal and the two lines it intersects. Here's a clear breakdown:
Position relative to the transversal: Corresponding angles are on the same side of the transversal, while alternate angles are on opposite sides.
Position relative to the other two lines: For corresponding angles, one angle is interior (between the lines) and the other is exterior (outside the lines). For alternate angles, both are either interior (alternate interior) or both are exterior (alternate exterior).
4. What does the Corresponding Angles Theorem state?
The Corresponding Angles Theorem, often treated as a postulate in geometry, states that if two parallel lines are intersected by a transversal, then the pairs of corresponding angles are equal (or congruent). The converse of this theorem is also true: if the corresponding angles are equal, then the two lines must be parallel.
5. Are corresponding angles equal only when the lines are parallel?
Yes, this is a crucial point. While corresponding angles are formed anytime a transversal intersects any two lines, they are only equal in measure if those two lines are parallel. If the lines are not parallel, the corresponding angles will exist, but their measures will not be equal. This property is a fundamental test for parallel lines in geometry.
6. Can you give a real-world example of where corresponding and alternate angles are used?
A perfect real-world example is in the design and construction of railway tracks. The two rails must be perfectly parallel. A transversal, like a railway tie or a crossing road, cuts across these rails. To ensure the rails are parallel, engineers can measure the alternate interior or corresponding angles. If these angles are equal, it confirms the tracks are parallel, ensuring the safety and stability of the train.
7. How does the Alternate Interior Angles Theorem relate to the Corresponding Angles Postulate?
The Alternate Interior Angles Theorem can be logically proven using the Corresponding Angles Postulate and the concept of vertically opposite angles. The steps are:
First, we state that a corresponding angle pair (let's say ∠1 and ∠5) are equal because the lines are parallel (Corresponding Angles Postulate).
Next, we observe that one of these angles (∠1) is vertically opposite to an alternate interior angle (let's say ∠3). Therefore, ∠1 = ∠3 (Vertically Opposite Angles).
Since ∠1 = ∠5 and ∠1 = ∠3, it follows that ∠3 = ∠5. This proves that the alternate interior angles are equal.
8. What is the importance of the converse of the Alternate and Corresponding Angle Theorems?
The importance of the converse theorems is their practical application in proving that two lines are parallel. While the original theorems start with the assumption that lines are parallel to determine angle relationships, the converse theorems work in reverse. If you can measure the angles formed by a transversal and show that a pair of corresponding or alternate interior angles are equal, you can definitively conclude that the lines are parallel. This is a fundamental tool used in geometric proofs, construction, and engineering to verify parallelism.























