Question

Define linear S.H.M. obtain a differential equation of linear S.H.M?

Answer 1

Hint: S.H.M stands for simple harmonic motion, it is described as the motion of a particle which moves back and forth along a straight line such that its acceleration is directly proportional to its displacement of the fixed point.

Complete answer:
Linear S.H.M is said to be the simplest form of the oscillatory motion in which a body when displaced from its mean position, oscillates ‘to and fro’ about mean position and the restoring force is always directed towards its mean position and its magnitude which is directly proportional to the displacement from the mean position.
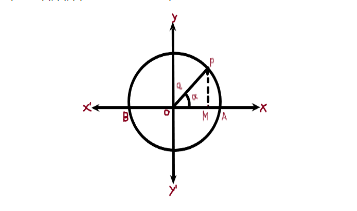
Now let us consider particles P moving along the circumference of a circle of radius ‘a’ with a uniform angular speed of $\omega $ in the anticlockwise direction.
Particle P along the circumference of the circle has its projection particle on diameter AB at point M. The projection particle follows linear S.H.M along line AB when particle P rotates around the circle.
Let the rotation start with the initial angle ‘a’ as shown above (t=0). In the time t the angle between OP and the axis will become $\omega t + \alpha $ as shown below:
Now from, $\vartriangle OPM = \dfrac{{OM}}{{OP}} = \cos (\omega t + \alpha )$
$\dfrac{x}{a} = \cos (\omega t + \alpha )$
$x = a\cos (\omega t + \alpha )$……………… (1)
Differentiating the above equation with respect to time
We get velocity
$v = \dfrac{{dx}}{{dt}} = - a\omega \sin (\omega t + \alpha )$ …………….. (2)
Differentiating again we get acceleration
 $a = \dfrac{{dv}}{{dt}} = \dfrac{{{d^2}x}}{{d{t^2}}} = - a{\omega ^2}\cos (\omega t + \alpha )$
$ \Rightarrow - {\omega ^2}x$……………….. (3) ($x = a\cos (\omega t + \alpha )$)

The equation (1), (2), (3) are the differential equation for the linear S.H.M.

Note:
Every oscillatory motion is the periodic but all periodic motions are not oscillatory. Therefore, the simple harmonic motion is the simplest type of oscillatory motion. This motion takes place when the restoring force is acting on a system.