Question

A window is in the form of a rectangle surmounted by a semi-circular opening. The total perimeter of the window is \[10m\]. Find the dimensions of the window to admit maximum light through the whole opening.

Answer 1

Hint:First, evaluate the perimeter of the figure and equate it to $10$. To admit maximum light through the whole opening we have to maximize the area of the figure to evaluate the dimensions of the window.

Complete step-by-step answer:
Draw the figure of the window.

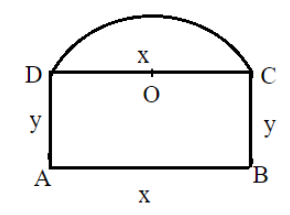
ABCD is the rectangle and O is the centre of the semi-circle.
We are given that a window is in the form of a rectangle surmounted by a semi-circle as shown in the figure.
First, we let the length and breadth of the rectangle.
Let $x$ and $y$ be the length and breadth of the rectangle respectively.
Since, the rectangle is surmounted by the semi-circle therefore, diameter of the semicircle is equal to the length of the rectangle.
Therefore, the diameter of the semicircle is $x$.
The radius is half of the diameter.
Therefore, the radius of the semicircle is $\dfrac{x}{2}$.
The perimeter of the whole figure includes two-time breadth, one-time length and the perimeter of the semicircle.
We know that the perimeter of the semicircle of radius $r$is $\pi r$.
Write the perimeter of the whole figure and equate it to $10$.
$x + 2y + \dfrac{{\pi x}}{2} = 10$
Solve for $y$.
$
  2x + 4y + \pi x = 20 \\
  4y = 20 - \pi x - 2x \\
  y = \dfrac{{20 - (\pi + 2)x}}{4}...........(1) \\
 $
Now we maximize the area of the window.
Let the area of the window is $A$ which is equal to the sum of the area of the rectangle and area of the semicircle.
Area of the rectangle is the product of the length and the breadth.
Area of the semicircle of radius $r$ is $\dfrac{{\pi {r^2}}}{2}$.
Therefore,
$A = xy \times \dfrac{1}{2}\pi {\left( {\dfrac{x}{2}} \right)^2}$
Substitute the value of $y$.
\[
  A = x\left[ {\dfrac{{20 - (\pi + 2)x}}{4}} \right] + \dfrac{{\pi {x^2}}}{8} \\
  A = \dfrac{{20x - (\pi + 2){x^2}}}{4} + \dfrac{{\pi {x^2}}}{8} \\
 \]
To maximize the area, differentiate $A$ with respect to $x$.
To maximize the area, differentiate with respect to .
Use $\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}$
$\dfrac{{dA}}{{dx}} = \dfrac{{20 - 2\left( {\pi + 2} \right)x}}{4} + \dfrac{{2\pi x}}{8}$…………..$(2)$
Equate it to $0$.
$
  \dfrac{{dA}}{{dx}} = 0 \\
  \dfrac{{20 - 2(\pi + 2)x}}{4} + \dfrac{{2\pi x}}{8} = 0 \\
  \dfrac{{20 - 2(\pi + 2)x}}{4} + \dfrac{{\pi x}}{4} = 0 \\
  20 - 2(\pi + 2)x + \pi x = 0 \\
  20 - 2\pi x - 4x + \pi x = 0 \\
  20 - \pi x - 4x = 0 \\
  20 - x(\pi + 4) = 0 \\
  x(\pi + 4) = 20 \\
  x = \dfrac{{20}}{{\pi + 4}} \\
 $
Differentiate equation $(2)$with respect to $x$
Use $\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}$
$
  \dfrac{{{d^2}A}}{{d{x^2}}} = \dfrac{{0 - 2(\pi + 2)}}{4} + \dfrac{\pi }{4} \\
  \dfrac{{{d^2}A}}{{d{x^2}}} = \dfrac{{0 - 2\pi - 4 + \pi }}{4} \\
  \dfrac{{{d^2}A}}{{d{x^2}}} = \dfrac{{ - \pi - 4}}{{\pi + 4}} \\
  \dfrac{{{d^2}A}}{{d{x^2}}} = \dfrac{{ - (\pi + 4)}}{{\pi + 4}} \\
  \dfrac{{{d^2}A}}{{d{x^2}}} = - 1 \\
 $
Since, at $x = \dfrac{{20}}{{\pi + 4}}$the value of \[\dfrac{{{d^2}A}}{{d{x^2}}} < 0\]therefore, the value of $A$ is maximum at $x = \dfrac{{20}}{{\pi + 4}}$.
Substitute the value of $x = \dfrac{{20}}{{\pi + 4}}$ in equation $(1)$.
$
  y = \dfrac{{20 - \left( {\pi + 2} \right)\dfrac{{20}}{{\pi + 4}}}}{4} \\
  y = \dfrac{{20\pi + 80 - 20\pi - 40}}{{4(\pi + 4)}} \\
  y = \dfrac{{10}}{{\pi + 4}} \\
 $
Radius of the semicircle is half of side DC
$\dfrac{x}{2} = \dfrac{{10}}{{\pi + 4}}$
Hence, the length and breadth of the rectangle is $\dfrac{{20}}{{\pi + 4}}$ and $\dfrac{{10}}{{\pi + 4}}$ respectively and radius of the semicircle is $\dfrac{{10}}{{\pi + 4}}$.

Note:
In these types of questions evaluate the one variable in terms of another variable to maximize the terms.
We use a double derivative test to find maximum and minimum value of the function. If the value of double derivative at critical points of the function is positive then minimum and when negative then maximum value occurs of the function.