Question

A person standing between two parallel hills fires a gun. He hears the first echo after 1.5 sec, and the second echo after 2.5 sec. If the speed of sound is 332 m/s, calculate the distance between the hills. When will you hear the third echo?

Answer 1

Hint: We are given the time taken for the first and second echo to be heard when a man fires a gun between two hills. The velocity of the sound is also given to us. We know the condition for us to hear an echo. Thus by applying the condition and using the equation connecting distance, speed, and time we will get the distance between man and two hills. The sum of the two distances will be the distance between two hills. By applying the condition to hear the third echo we will get the time taken for it to be heard.

Formula used:
$\text{distance=speed }\!\!\times\!\!\text{ time}$

Complete step-by-step solution
In the question, we have a man firing a gun from between two parallel hills.
The figure below shows the given situation.

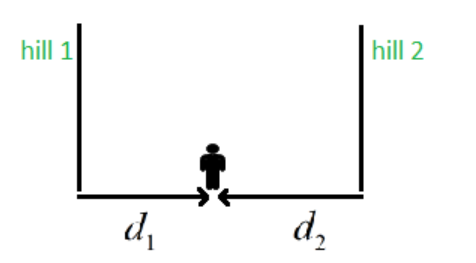
Let the distance between man and hill 1 be ‘${{d}_{1}}$’ and the distance between man and hill 2 be ‘${{d}_{2}}$’.
It is said that the time taken for the first echo to be heard is 1.5 seconds.
Let this time be ‘${{t}_{1}}$’. Therefore,
${{t}_{1}}=1.5\sec $
We know that the first echo would be heard when the sound travels from the man to the hill 1 and returns to the man.
Thus the distance traveled in the first echo will be $2{{d}_{1}}$.
The velocity of the sound is also given to us as 332 m/s.
We know that,
$\text{distance=speed }\!\!\times\!\!\text{ time}$
Therefore we can write,
$\Rightarrow 2{{d}_{1}}=v\times {{t}_{1}}$
$\Rightarrow 2{{d}_{1}}=332\times 1.5$
From this we will get the distance between man and the hill 1 as,
$\Rightarrow {{d}_{1}}=\dfrac{332\times 1.5}{2}$
$\Rightarrow {{d}_{1}}=249m$.
Thus the distance between man and the hill 1 is 249m.
Similarly we can write the hill and man as,
$2{{d}_{2}}=v\times {{t}_{2}}$
The time taken for the second echo to be heard is given as, ${{t}_{2}}=2.5\sec $
Therefore the distance between the man and the hill 2 will be,
$\Rightarrow 2{{d}_{2}}=332\times 2.5$
$\Rightarrow {{d}_{2}}=\dfrac{332\times 2.5}{2}$
$\Rightarrow {{d}_{2}}=415m$
We are asked to find the total distance between the two hills.
The total distance between the two hills can be given as,
${{d}_{1}}+{{d}_{2}}$
$\Rightarrow 249+415$
$\Rightarrow 664m$
Hence the distance between the two hills is 664m.
We also need to find the time taken to hear the third echo.
We know that the third echo will be heard when the sound from the person after reflecting from the first hill moves toward the second hill and reflects back to the person.
Therefore the time taken for the third echo to be heard will be the sum of the time taken by the first and second echo.
$\Rightarrow {{t}_{3}}={{t}_{1}}+{{t}_{2}}$, were ‘${{t}_{3}}$’ is the time taken for the third echo to be heard.
\[\Rightarrow {{t}_{3}}=1.5+2.5=4\sec \]
Hence the time taken for the third echo to be heard is 4 seconds.

Note: Sound gets reflected on solid or liquid surfaces. Due to the reflection of sound, we hear the original and the reflected sound more than once. This phenomenon of sound is called echo. For an echo to be heard distinctly the minimum distance between the source and the reflecting surface should be 17.2m.